La transformada de Laplace recibe su nombre en honor del matemático francés Pierre Simon Marquéz de Laplace, fue un matemático y astrónomo francés tan famoso en su tiempo que se le conocía como el Newton de Francia.
DEFINICIÓN
Es una herramienta matemática de gran alcance formulada para solucionar una variedad amplia de problemas del inicial-valor. La estrategia es transformar las ecuaciones diferenciales difíciles en los problemas simples de la álgebra donde las soluciones pueden ser obtenidas fácilmente.
En comparación con los métodos clásicos de solución de ecuaciones diferenciales, el método de Laplace se basa en:
Las soluciones, tanto homogénea como particular de las ecuaciones diferenciales, se obtienen en una sola operación matemática
La transformada de Laplace convierte la ecuación diferencial en ecuaciones algebraicas con el operador s, por lo que es posible manipular las mismas mediante las reglas básicas del álgebra para obtener la solución, la cual se obtiene tomando la transformada inversa de Laplace
La transformada de Laplace es la función
definida mediante la integral:
Nota:
La transformada de Laplace convierte una función en t en una función en la variable s, la cual para el proceso de integración se considera constante
Las condiciones para la existencia de la transformada de una función, son:
Ser de orden exponencial
Estar definida y ser continua a pedazos en el intervalo
PROPIEDADES DE LA TRANSFORMADA
Linealidad
Primer Teorema de Traslación
La transformada de Laplace se convierte un factor exponencial en una traslación en la variable s.
Teorema de la Transformada de la Derivada
Teorema de la Transformada de la Integral
Teorema de la Integral de la Transformada
Teorema de la Derivada de la Transformada
Transformada de la Función Escalón
Segundo Teorema de Traslación
Transformada de una Función Periódica
Teorema de la Convolución
APLICACIÓN PARA EL CONTROL DE PROCESOS
En muchos procesos de la vida diaria está involucrada la Transformada de Laplace, ya que, es una forma precisa y directa utilizada en el control de dichos procesos, como, por ejemplo: en el ámbito doméstico para controlar la temperatura y humedad de las casas y edificios; en la transportación para controlar que un automóvil o avión se muevan de un lugar a otro en forma segura y exacta y en la industria para controlar múltiples variables en los procesos de manufactura.
En el estudio de los procesos es necesario considerar modelos dinámicos, es decir, modelos de comportamiento variable respecto al tiempo. Esto trae como consecuencia el uso de ecuaciones diferenciales respecto al tiempo para representar matemáticamente el comportamiento de un proceso. El comportamiento dinámico de los procesos en la naturaleza puede representarse de manera aproximada por el siguiente modelo general de comportamiento dinámico lineal:
La transformada de Laplace es una herramienta matemática muy útil para el análisis de sistemas dinámicos lineales.
Una vez que se ha estudiado el comportamiento de los sistemas dinámicos, se puede proceder a diseñar y analizar los sistemas de control de manera simple.
APLICACIÓN DE LA TABLA
EJERCICIO APLICADO EN CONTROL DE PROCESOS
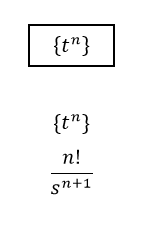
Comentarios